Automatic Occluder Generation

Properties of occluders
Occluders are a variant, or alternative representation of a mesh. They are an essential part of an occlusion culling system, as their simplified representation allows the occlusion step to be more efficient than if it were to use the original and high definition version of the mesh. To leverage them, they have to respect a few properties.
Reduced complexity in comparison to the original mesh, in terms of triangle count and shape. Occluders should be fast to draw. This can be done by using an aggregate of simpler convex shapes.
Conservative; its volume should be less than or equal to the original mesh volume and contained within. This property is required to prevent false positive, or discarding objects from the visible set. Conservative occluders may allow for pre-z optimization as drawing them in a depth only render pass prior to any fragment-costly shaders could leverage the hardware hierarchical z-culling and/or early z fragment rejection.
Large; fills the largest possible volume of the original mesh. This property guarantees that the mesh would discard as many elements as if the original mesh was used. To calculate the mesh efficiency, it could be imagined to render both the occluders and its original mesh and see if the rejection ratio of using one or the other is reaching a satisfying convergence. This property can be viewed in terms of having a high screen-area coverage from different viewpoints. It is important to note that depending on which side your mesh will be drawn, it is possible to make specific optimizations therein. For example, in a car driving simulation where the viewpoint is known to be on the ground; a boxed-shape building would likely be simplified as a box occluder where the box is composed side faces, without the top and bottom. This would differ in an open-world game, where the level of freedom reduces the ability to make such assumptions.
Automatic generation of occluders
The algorithm chosen to automatically generate occluders takes in a 3d mesh, and outputs a list of AABBs ensured to be contained within the input 3d mesh. It is composed of 4 main steps:
- Shell voxelization
- Inner voxelization using the previously generated shell voxel set
- Generate a per-axis minimum distance to shell voxel from each voxel in the inner voxel set
- Iterative box expansion using the per-axis minimum distances starting from voxels in the inner set
For comprehension, the algorithm will be first illustrated and described in 2d, and then extended to the 3d case. Note that the algorithm described in 2d is a simplification of the 3d algorithm and would likely be optimized accordingly if it was used in 2d.
Box filling algorithm in 2D
In 2d, voxelization is commonly named rasterization, and a voxel a pixel. The first two steps of the algorithm are shell and inner rasterization (known as conservative rasterization). In order to simplify things, the mesh is represented by a single triangle. And instead of performing triangle-cube intersection, as we will see in 3d, we perform triangle-edge intersection against pixel-aligned AABBs.
Shell and inner conservative pixelization
To be able to generate a conservative set of pixels, we need to first generate the shell pixel set. To do so, we snap the triangle AABB to the pixel grid; pixel snapping is the process of mapping any 2d position to a single pixel. Then, iterate over each pixel of that grid and perform triangle-edge to AABB intersection. This gives the first set of shell pixels (in blue in the figure below).
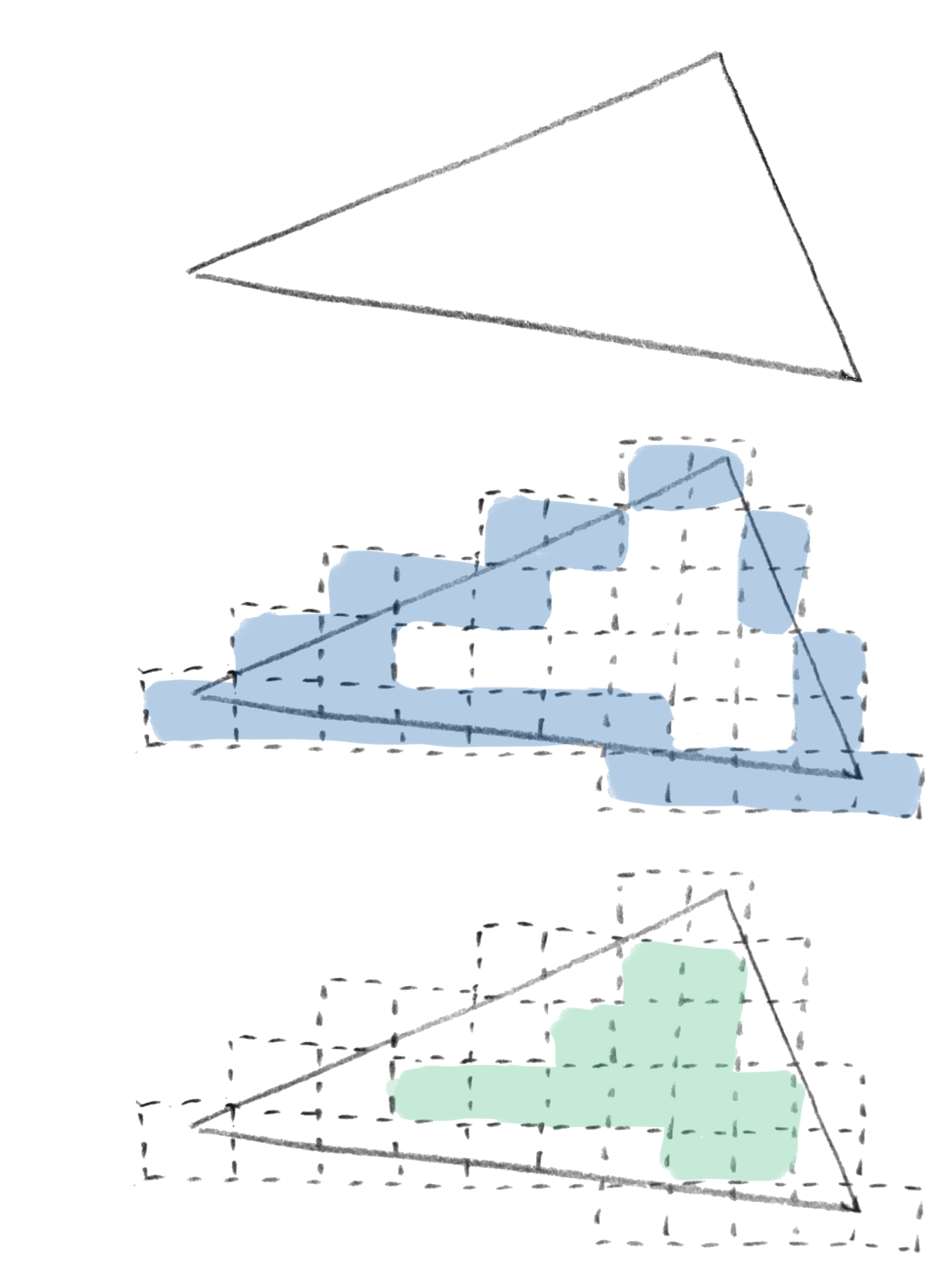
Once the shell pixel set is available, we perform a second pass over the pixel grid covered by the triangle, and look in each positive and negative direction of the unit axes, $(+x, 0)$, $(-x, 0)$, $(0, +y)$, $(0, -y)$. If from a given pixel, there are 4 shell pixels visible from all these directions, the pixel is marked as part of the inner pixel set; this performs conservative rasterization.
Minimum distance to shell pixel (On the positive unit axes)
The next step of the algorithm takes in both the shell and inner pixel set, and calculates the minimum distance to shell pixel for each pixel of the inner pixel set. The distances are calculated for the positive axis. The reason being that when doing the next expansion step, the expansion will be done in both the $(+x, 0)$ and $(0, +y)$ directions.
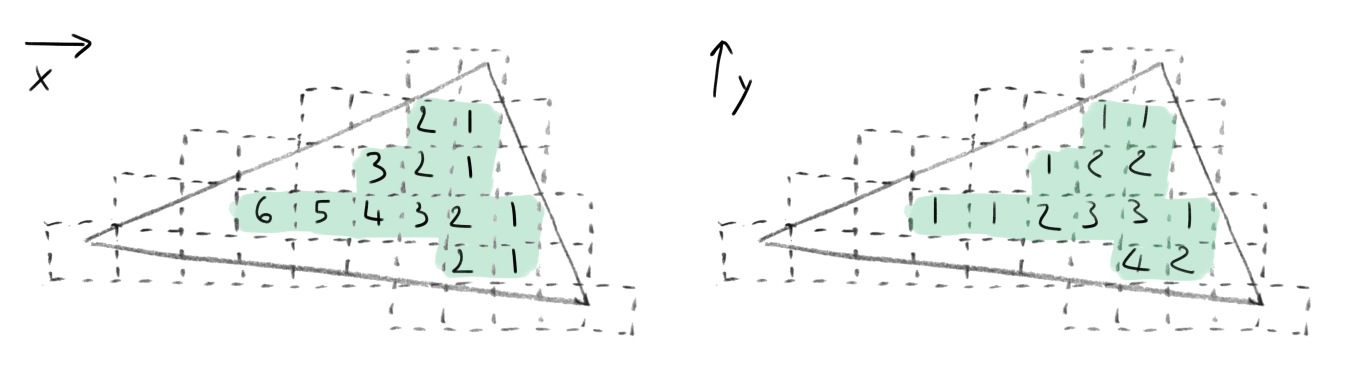
In the provided source code, this step is in fact done when marking the pixels as part of the inner pixel set as an optimization.
Box expansion on positive unit axes
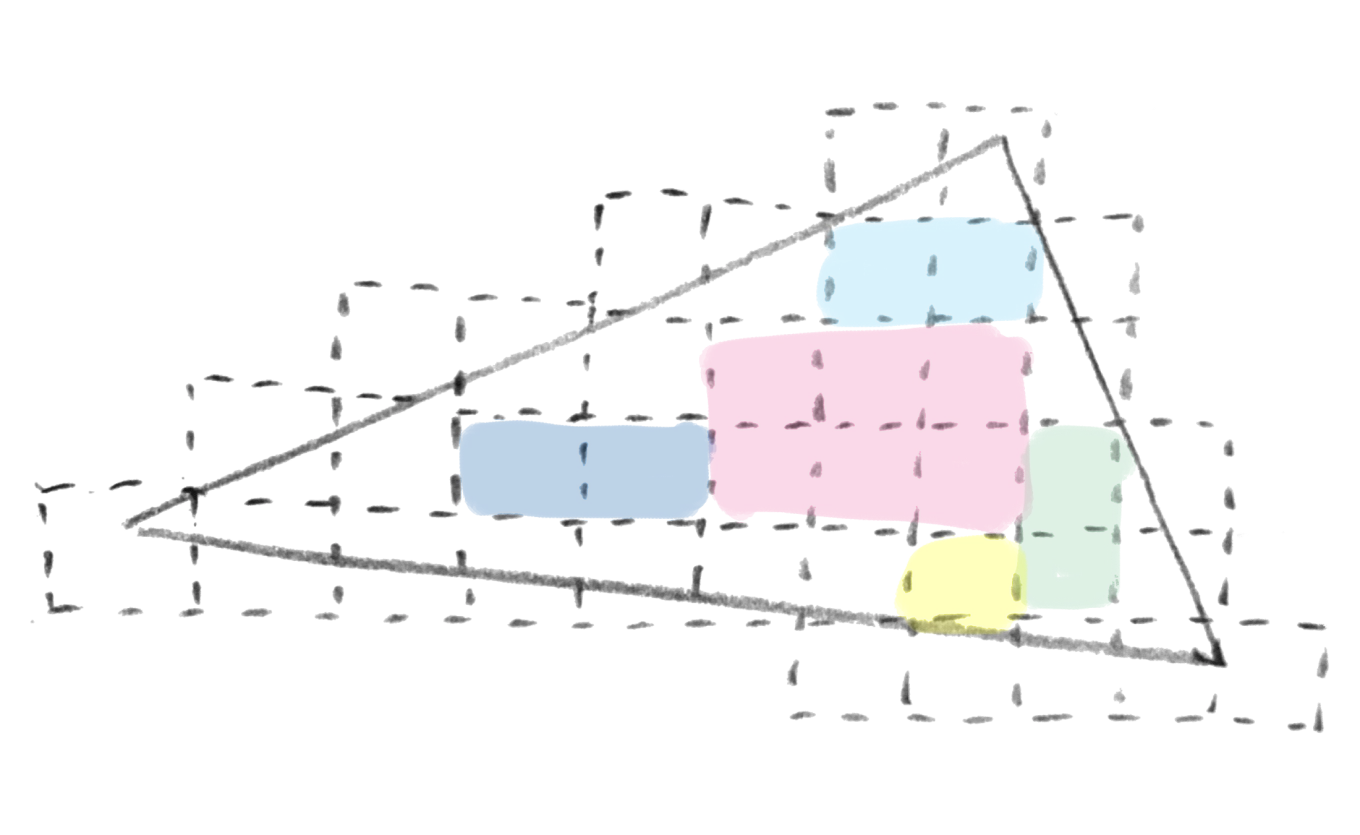
At this point, we have all the data necessary to iteratively perform AABB expansion. At each step of the iterative process, the idea is to find the AABB which maximizes the covered area the most (or volume in 3d) and then clip that AABB to the inner pixel set before repeating. The clipping ensures that we reject any processed pixel for the next iteration.
One step to find the maximized AABB area can be described as follows: For a given inner pixel at $(x, y)$ and its minimum distances to shell pixel $d_{x}$ and $d_{y}$ on the respective positive $x$ and $y$ unit axes, retrieve all inner pixels within the range $(x, y)$ to $(x, y + d_{y} - 1)$ and find $max(area(d_{y}, d'_{x}))$, where $d'_{x}$ is the minimum distance on $x$ for any inner pixel of the described range. This both maximizes the covered area of an AABB that would expand from $(x, y)$ and ensures the non-overlap with the set of shell pixels.
Now that we have a way to find the AABB that maximizes the covered area for any given inner pixel at $(x, y)$ we can find the pixel that maximizes the area for the current set of inner pixels using the method previously described. Then, clip all inner pixels that lay within the extent of the chosen AABB, and repeat the process again. We can stop the process when the sum area of all the AABBs reached a given percentage of the triangle area.
Box filling algorithm in 3D
To perform voxelization and generate the shell voxel set, Akenine-Moller triangle-cube intersection is performed for the voxels covered by the 3d grid of the triangles. Note that similarly to 2d, the triangle is snapped to the voxel grid for a given voxel resolution.
We can then use the shell voxel set, to do visibility test and distance field generation; a voxel is marked as belonging to the inner voxel set, if and only if it can see a voxel in the shell voxel set on each of the unit axes $x$, $y$, $z$ in both the positive and negative direction. To give intuition, imagine being in a room, you can convey yourself that you are inside if there is a wall/floor in front, behind, on the right, left, on top and beneath you. An inner voxel sees another shell voxel on the positive unit axes, the distance to that voxel is updated if it is smaller than the currently stored distance. Only positive axes are used for distances as they are the extension direction used during the filling phase, similarly to the 2d case.

The box expansion is the same as in 2d, with the exception that another axis must be iterated over when selecting the volume that maximizes the current iteration. In 3d, the mesh volume is approximated by the number of inner voxels it contains, which is a common approximation when trying to find the volume of a mesh. Note that this approximation is better the higher the voxel resolution is. The box expansion process stops when the total volume of selected AABBs reaches a reasonable percentage of the total volume of the mesh.
The documented source code is available on github.
The source code for the embedded example in this webpage is available here.